Valószínűség-számítás

MS-3255

Valószínűség-számítás tankönyv

11-12. évfolyam, 1. kiadás (2009. 01. 30.)

Mozaik Kiadó

szerző: Ábrahám István Dr.

méret: 170x240 mm

terjedelem: 120 oldal

Tartalom Mintaoldalak

2 280 Ft

Kosárba

A valószínűség-számítás gyakorlati alkalmazásába bevezető stúdiumok tanulásához készült tankönyv elsősorban a nem matematikai irányban tanuló főiskolai és egyetemi hallgatóknak nyújthat segítséget. A könyv a témától idegenkedő hallgatók számára a lehető legegyszerűbb, lényegre törő, praktikus megközelítésmódot alkalmaz, így segíti a valószínűség-számítás alapjainak elsajátítását.
A könyvhöz hasonló stílusú feladatgyűjtemény is tartozik.

Kapcsolódó kiadványok

Valószínűség-számítás összefoglaló feladatgyűjtemény - MS-3256

Mintaoldalak

Tartalomjegyzék

Kombinatorika	7
Permutáció	7
Ismétlés nélküli permutáció	7
Ismétléses permutáció	9
Variáció	10
Ismétlés nélküli variáció	10
Ismétléses variáció	12
Kombináció	13
Ismétlés nélküli kombináció	13
Ismétléses kombináció	14
A kombinációs számok tulajdonságai	16
A binomiális tétel	17
Mintapéldák	19
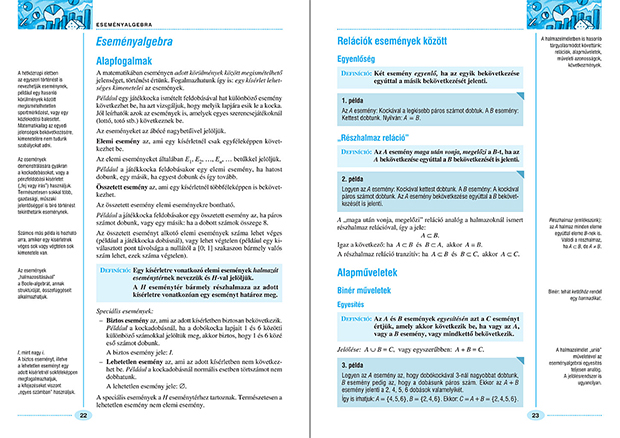
Eseményalgebra	22
Alapfogalmak	22
Relációk események között	23
Egyenlőség	23
"Részhalmaz reláció"	23
Alapműveletek	23
Binér műveletek	23
Egyesítés	23
Közös rész képzés	24
Unáris műveletek	24
Komplementer képzés	24
Az alapműveletek azonosságai	25
További műveletek	25
További műveleti azonosságok	26
De Morgan azonosság	26
További fogalmak, tételek	26
Klasszikus valószínűség-számítás	29
A valószínűség fogalma és axiómái	29
A valószínűség-számítás axiómái	29
Az axiómákból következő tételek	30
Mintavételi feladatok	33
Visszatevés nélküli mintavétel	33
Visszatevéses mintavétel	34
A feltételes valószínűség	36
Két esemény szorzatának valószínűsége	37
A teljes valószínűség tétele	37
Bayes-tétel	39
Az események függetlensége	40
Független kísérletsorozat Bernoulli-féle képlete	42
Valószínűségi változók	44
Alapfogalmak	44
Az eloszlásfüggvény	46
Az eloszlásfüggvény tulajdonságai	48
A sűrűségfüggvény	50
A sűrűségfüggvény tulajdonságai	52
Valószínűség-eloszlások a gyakorlatban	54
Diszkrét eloszlások	54
Egyenletes eloszlás	54
Hipergeometrikus eloszlás	55
Binomiális eloszlás	56
Poisson-eloszlás	57
Geometriai eloszlás	59
A karakterisztikus eloszlás	60
Folytonos eloszlások	61
Egyenletes eloszlás	61
Exponenciális eloszlás	62
Normális eloszlás	64
A valószínűségi változó jellemzői	67
A várható érték	67
A szórás	69
A módusz, a medián és a kvantilisek	71
A módusz	71
A medián	72
A kvantilisek	73
Néhány konkrét valószínűség-eloszlás jellemzői	74
Diszkrét eloszlások	74
Egyenletes eloszlás	74
Hipergeometriai eloszlás	74
Binomiális eloszlás	75
Poisson-eloszlás	76
Geometriai eloszlás	77
Karakterisztikus eloszlás	78
Folytonos eloszlások	78
Egyenletes eloszlás	78
Exponenciális eloszlás	80
Normális eloszlás	81
A nagy számok törvényei	83
A Markov-egyenlőtlenség	83
A Csebisev-egyenlőtlenség	84
A nagy számok törvénye binomiális eloszlásra (a Bernoulli-féle alak)	85
Kétdimenziós eloszlások	89
A kétdimenziós eloszlás megadása	89
Diszkrét kétdimenziós eloszlás	89
Folytonos kétdimenziós eloszlás	92
Nevezetes kétdimenziós folytonos valószínűség-eloszlások	93
Kétdimenziós eloszlásfüggvény	94
Az együttes eloszlásfüggvény tulajdonságai	96
Az együttes eloszlásfüggvény és az együttes sűrűségfüggvény kapcsolata	96
Perem-eloszlásfüggvények	99
A kétdimenziós valószínűségi változók jellemzői	104
Kovariancia és korrelációs együttható	104
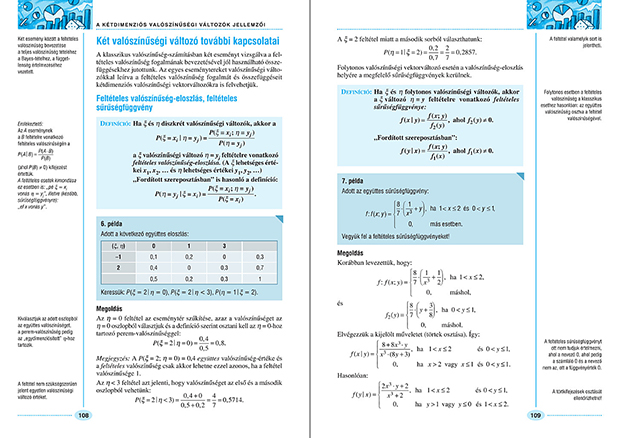
Két valószínűségi változó további kapcsolatai	108
Feltételes valószínűség-eloszlás, feltételes sűrűségfüggvény	108
Függetlenség	110
Regresszió	112

A kiadvány bevezetője

A valószínűség-számítás a tudományok egyik legősibb, ugyanakkor legfiatalabb ága. Az ember ugyanis kezdetektől fogva tudni akart valami biztosat a bizonytalanról, a véletlenszerűen bekövetkező eseményekről. Hírneves és hírhedt „tudós” jósok próbáltak jövendölni, szerencsejátékosok számolgatták évszázadok óta a nyerési esélyeiket, különböző tudományterületek képviselői kutatták a a véletlentől függő (szochasztikus) folyamatokat és találtak is bizonyos szabályszerűségeket. Igazi nagy tudományos eredmények a valószínűségek kiszámolására, az elméleti összefüggések felvételére csak a 20. században születtek. 1933-ban Kolmogorov orosz matematikus megadta a valószínűség-számítás axiómáit, amelyekre azóta egy rendkívül szerteágazó elmélet épült és fejlődik jelenleg is, valamint jelentős gyakorlati alkalmazások bizonyították az elmélet helyességét. Világszerte elismert kutatásokkal gazdagították a valószínűség-számítást magyar matematikusok is, mint például Jordán Károly és Rényi Alfréd.

A valószínűség-számítás két nagyobb részre bontható. A klasszikus valószínűség-számítás eredményeinek nagy része ismert volt az axiomatizálás előtt is. Ide tartoznak a kombinatorika egyszerűbb összefüggései, a Boole-algebra eseményekre történő alkalmazása, valamint a számolásokban gyakran használt képlet, amely szerint úgy kapjuk meg egy esemény valószínűségét, hogy a kedvező esetek számát elosztjuk az észlelt összes eset számával. Az axiómákra építve a klasszikus valószínűség-számítás egységes rendszerben tárgyalható. A valószínűségi változók bevezetése lényegében a sztochasztikus folyamatok leírásában a „függvényesítést” jelenti. Ezzel a függvénytan apparátusát vetjük be a véletlenek matematikájába és kapunk érdekes elméleti, valamint jól alkalmazható gyakorlati eredményeket. A fentiekből is következően a valószínűség-számítás alapjainak elsajátításához szükségünk lesz a kombinatorika, az eseményalgebra tárgyalására, a függvénytani ismeretekre, jó számolókészségre valamint a problémamegoldáshoz a feladatok modellezésére, a saját józan eszünkre. A valószínűség-számítás eredményeit egyre inkább használják a különböző szaktudományokban, különösen a közgazdasági és műszaki területeken.

Nézz körül itt is!

Valószínűség-számítás

Valószínűség-számítás tankönyv